Ali Kaya
It was finally the weekend! After my long mathematics presentation, I came home to watch my favorite tv show, Person of Interest, to de-stress. Surprisingly, the episode was about the most famous mathematical constant, pi (π) which is equal to the ratio of a circle’s circumference to its diameter, commonly approximated as 3.14159. Mr. Finch (the main character) was acting as a substitute teacher and wrote on the chalkboard 3.1415926535. Then he asked the students, “What does this mean?” I answered the question in my mind, thinking, “If I have a bicycle tire with a diameter of 1, then one full revolution of the bicycle tire would travel the distance pi.” However, in the show, nobody answered. Then Mr. Finch answered the question himself, saying:
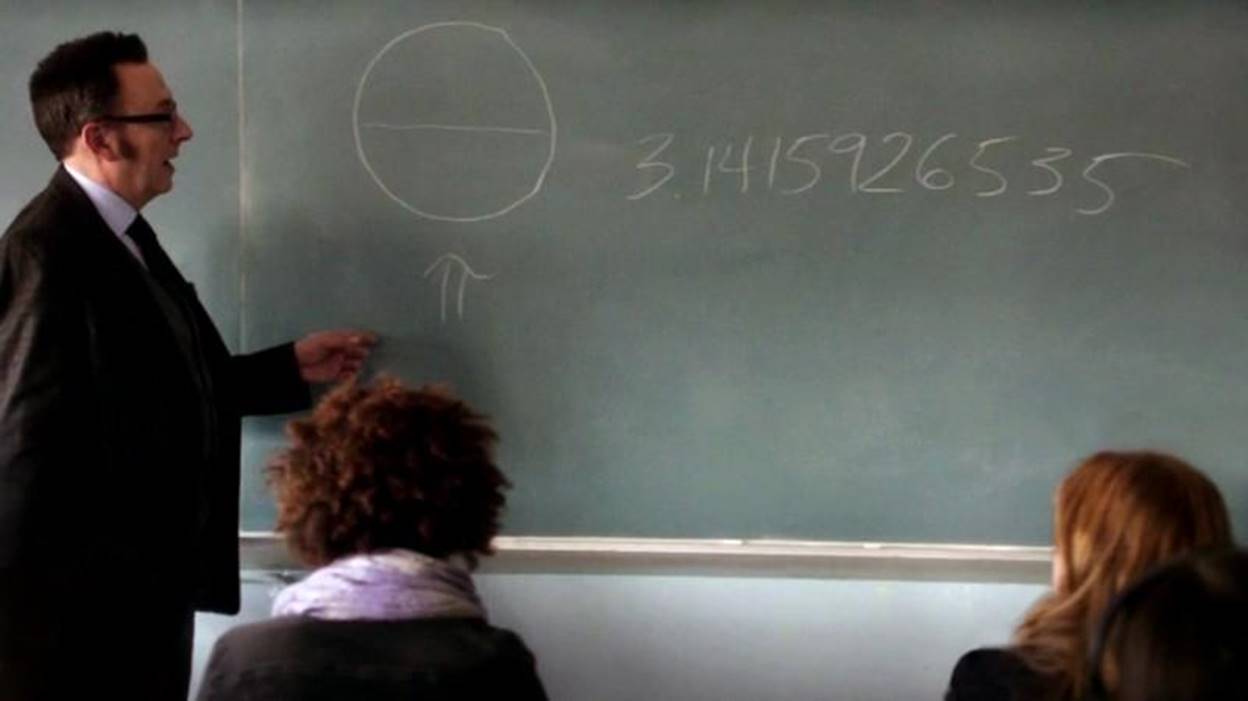
Person of Interest, Season 2 Episode 11 “2 Pi R”
“Pi, the ratio of the circumference of a circle to its diameter — 3.1415926535 — is just the beginning. It keeps going forever without ever repeating, which means that contained within this string of decimals is every other number; your birth date, the combination to your locker, your social security number, etc. It’s all in there somewhere. And if you convert these decimals into letters you would have every word that ever existed in every possible combination; the first syllable you spoke as a baby, the name of your latest crush, your entire life story from beginning to end, and everything we ever say or do. All of the world’s infinite possibilities rest within this one simple circle. Now what will you do with that information; what it’s good for? Well, that would be up to you…”
Although that scene was actually inaccurate, I loved it. This scene is beautiful because most teachers in the world struggle to be as good and as interesting of a teacher as Mr. Finch is here. His knowledge about the subject expands the discussion beyond the textbooks and keeps the students focused throughout the lecture.
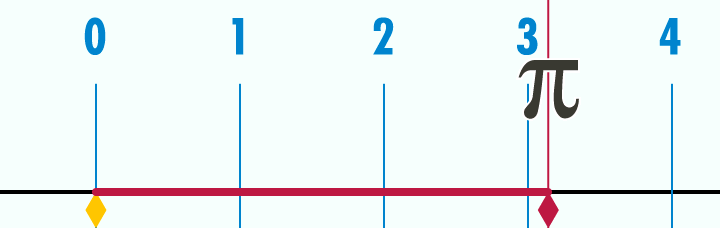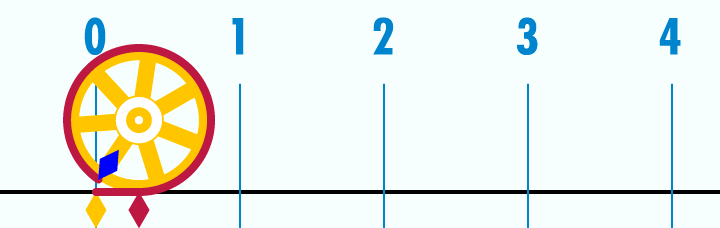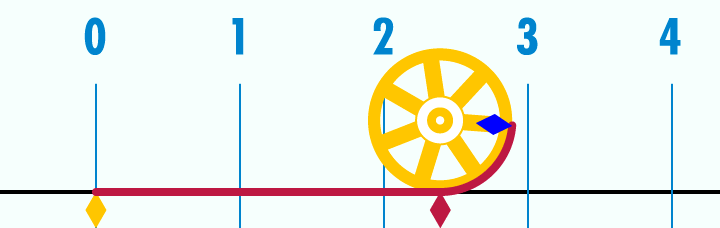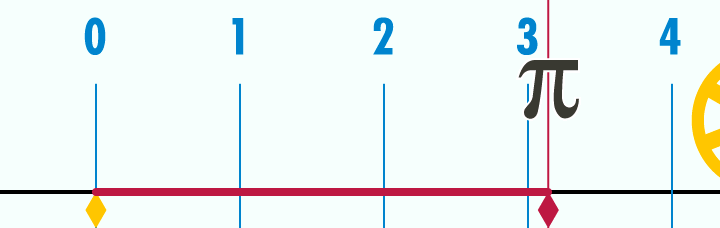
Wikipedia, gif, “Pi Unrolled”
We have all been taught that pi is the ratio of a circle’s circumference to its diameter.
Unfortunately, this is wrong because mathematicians have not proved that pi has the characteristic of “normality” yet. In other words, mathematicians are not sure if pi contains all the finitely long permutations of digits from 0 to 9. They are not sure if every digit continues to be used after a certain amount of time or an unlimited number of times in pi’s decimal representation. Nobody knows what we will find in the digits of pi if we keep going. For instance, when we check the first billion digits of pi, we see that the digit 7 occurs almost 100 million times. This makes pi a nice random number generator. However, after some points, pi may not contain the digit 7 and might instead have a non-repeating number with just two or three digits such as 010203112233000111222333…
For instance, after the first 761 digits of pi, there is a famous mathematical coincidence where six nines occur in a row which is called the Feynman point.
Twitter, Feynman’s Library, “Feynman Point in Pi”
But we are sure that the digits of pi keep going on forever and in a random order. This makes pi interesting because the value of pi is finite; however, its decimal value is infinitely long. This is not a contradiction. Pi is a constant number because it is the ratio of the circumference of a circle and its diameter, which are finite values. Still, we need an approximate value for pi.
In 1768, Johann Lambert proved that the value of pi is an irrational number and it cannot be written as a rational simple fraction. 22/7 is a commonly used approximation but does not contain all of the digits of pi. This is because irrational numbers cannot be written as a ratio of two numbers, such as ![]() , because they continue on to infinity and do not follow a pattern. In 1882, Ferdinand Lindemann proved that pi is a transcendental number because it is not algebraic; it is not a non-constant polynomial equation with rational coefficients (“Transcendental number”, Wikipedia).
, because they continue on to infinity and do not follow a pattern. In 1882, Ferdinand Lindemann proved that pi is a transcendental number because it is not algebraic; it is not a non-constant polynomial equation with rational coefficients (“Transcendental number”, Wikipedia).
We can safely say that pi is transcendental because the mathematician Yasumasa Kanada found that the first trillion digits of pi appear to be statistically random. If you check the table below, you see that the event of each digit occurring is independent, and the probability of it is one-tenth of the time (“Kanada Laboratory,” Super Computing)
|
Digit |
Occurrences |
|
0 |
99,999,485,134 |
|
1 |
99,999,945,664 |
|
2 |
100,000,480,057 |
|
3 |
99,999,787,805 |
|
4 |
100,000,357,857 |
|
5 |
99,999,671,008 |
|
6 |
99,999,807,503 |
|
7 |
99,999,818,723 |
|
8 |
100,000,791,469 |
|
9 |
99,999,854,780 |
|
Total |
1,000,000,000,000 |
After many years, Emma Haruko Iwao found 34.1 trillion digits of pi in 2019. It took 121 days for Haruko and his computer, because calculating pi requires a lot of power, even for a computer. You can picture it in your mind like this; if you were to print a billion decimal values of Pi in normal sized, ordinary font, it would stretch from New York to Kansas.
However, 34.1 trillion digits is still not enough to prove whether pi is normal or not (“Pi in the Sky, Google Cloud Blog). Supercomputers are still crunching the numbers. If you check the graph below, you will see the number of known digits of pi, by year, since 250 B.C.
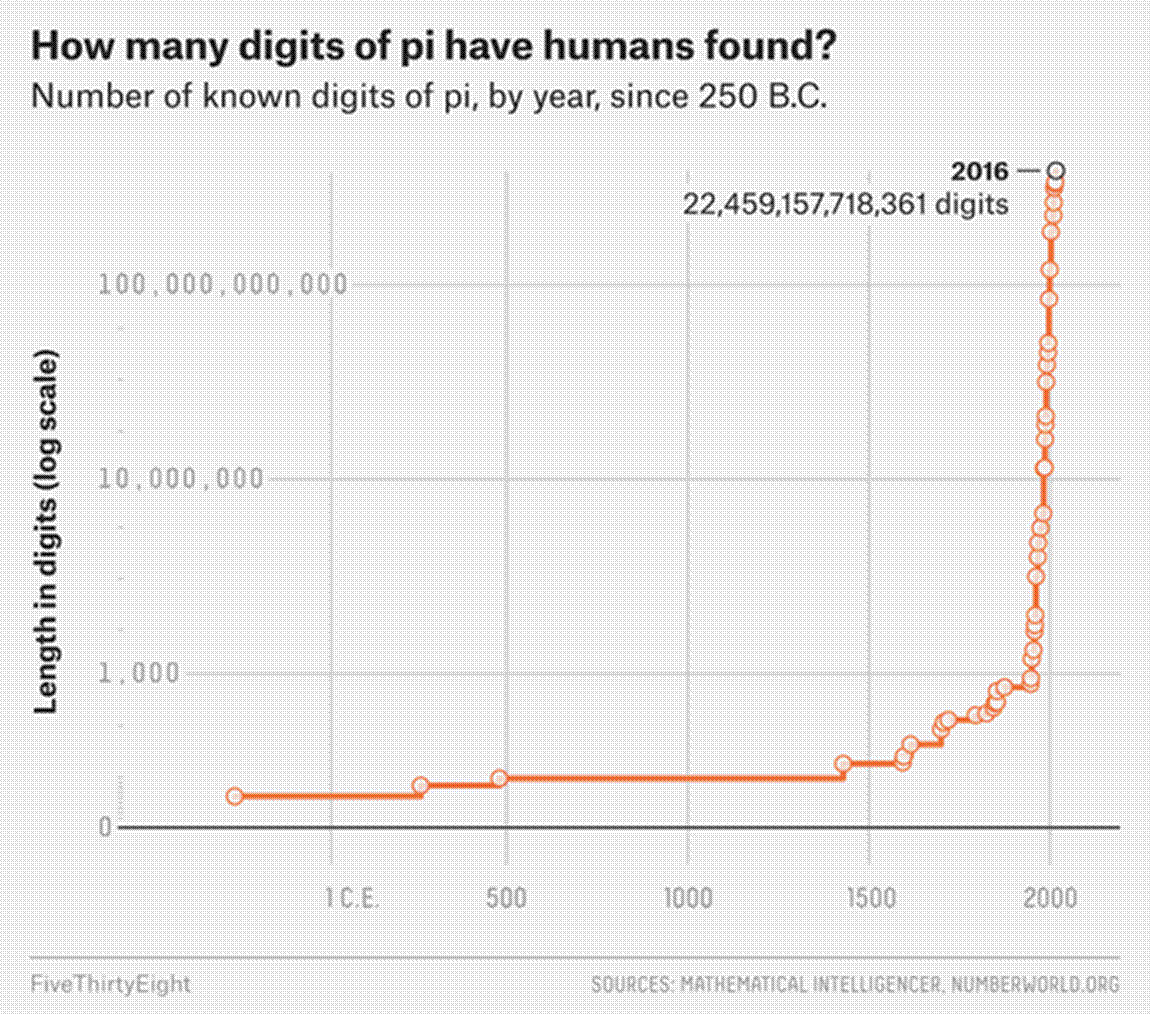
FiveThirtyEight, Graph, “Even After 31 Trillion Digits, We’re Still No Closer To The End Of Pi”
Going back to Mr. Finch, we see that he is not 100% wrong. We can find our birthdays in pi easily. If you go to mypiday.com and type your birthday, it will give you the decimal place in pi. For example, my birthday occurs at the 675,097th decimal place.
If pi is a normal number, then we can say that our whole destiny is encoded in pi. The pictures we are going to take in the future, will be in pi because there are binary numbers behind images. All digital products are in pi. Even this article has been in pi for thousands of years. Furthermore, the DNA of every creature is in pi. Mr. Finch was actually right.
There is an interesting and artistic way to show the randomness of pi. Some scientists might be happy with their tedious scatter plots, but there are some artists who use colors for data visualization to communicate with the public. Martin Krzywinski is one such artist, who found beauty and artistry in the randomness of Pi. He took the digits of pi and gave each digit a different color. For instance, he gave 3 the color orange, 1 as red, 4 as yellow, and so on. Then he made a beautiful poster. And if you look at it carefully, you do not see any particular pattern to the colors.

Science Art by Martin Krzywinski
Should we stop working on pi? Or should we continue looking for a better approximation? Is assuming pi as equal to 3.14 good enough? Or is it enough to use 40 digits of pi to find the circumference of the Milky Way galaxy to an error less than the size of a proton (JPL NASA)? Are the first 152 digits enough to find the circumference of the observable universe at 93 billion light-years (WIRED)? There are hundreds of mathematicians who have been trying to figure out more digits of pi for years. It is like trying to get to the moon and then to the next planet, and so on…
But why? Why do mathematicians bother calculating any more digits? Why aren’t 34.1 trillion digits of pi enough? Is it because pi lurks in every circle?
The logical reason seems cryptic: is it because pi is a beautiful source to generate random numbers? Or is it that countries can show off their technology to other countries, because calculating trillions of digits of pi requires a very powerful computer? For instance, in the Star Trek episode “Wolf in the Fold,” Spock foils the evil computer by commanding it to “compute to last digit of the value of pi.” So asking a computer to compute pi is called “a stress test” and may make it crash.
On the other hand, we humans are just weird. Staying at home and drinking tea is a beautiful activity, but when we get bored, we try to climb the highest of mountains, befriend a tiger, or try to memorize the digits of pi, like Chao Lu, who correctly memorized the first 67,890 digits of pi. We will keep doing these things because we like to understand the world around us.
We are inevitably connected to the past, and pi is a thread that’s gone through all of human history. That’s why we can say that as long as there are people, there’s always going to be somebody who wonders what’s next. And I assure you that somewhere in the world there is a mathematician or scientist using pi for something important, because pi is still the mysterious constant of nature.
Finding Pi
The previous statement is utterly true: there has always been someone who works on pi. Math is as old as civilization. Pi has been studied by the human race for almost 4000 years. When the last mammoths were going extinct, people were studying Pi. As far as we know, Archimedes was one of the first humans who calculated pi. He was most likely helping wheel makers. But how did he estimate the value of pi?
Firstly, he saw that all polygons are a circle. According to Archimedes, if you keep increasing the number of the sides of a polygon, you get closer to the perfect circle. In other words, a pentagon is more circle than a square, but a hexagon is more circle than a pentagon, and so on… Thus, more than two thousand years ago, he defined a circle as a regular polygon with an extremely large number of sides.
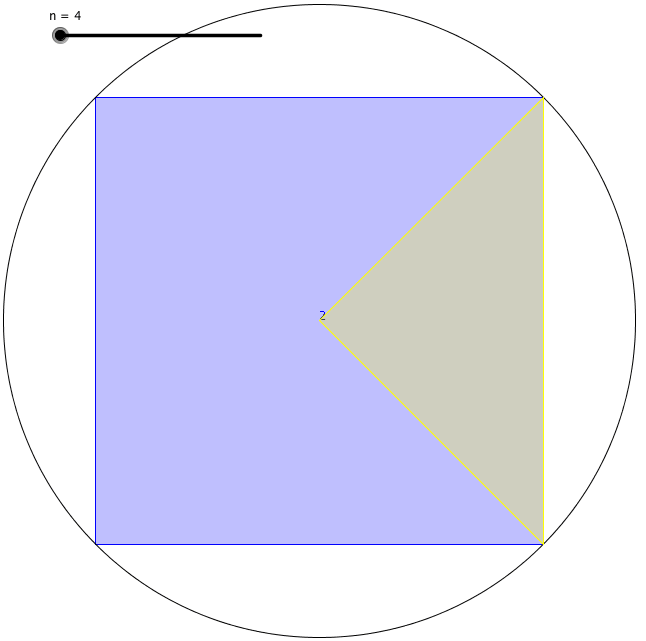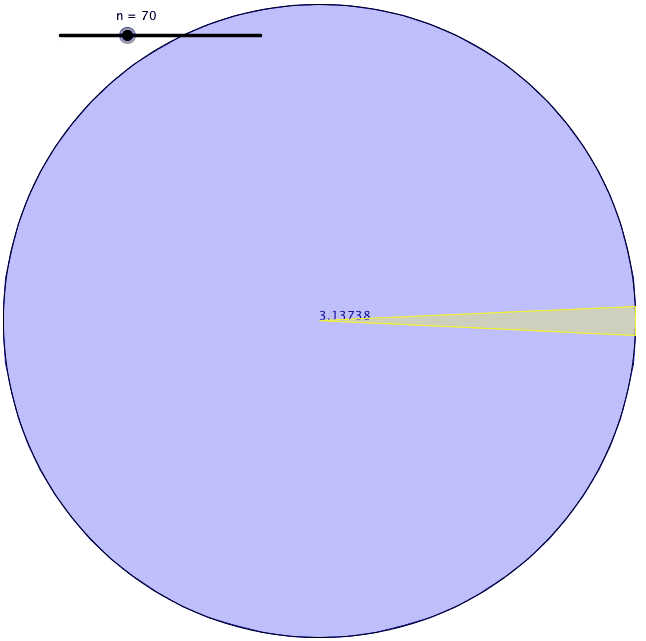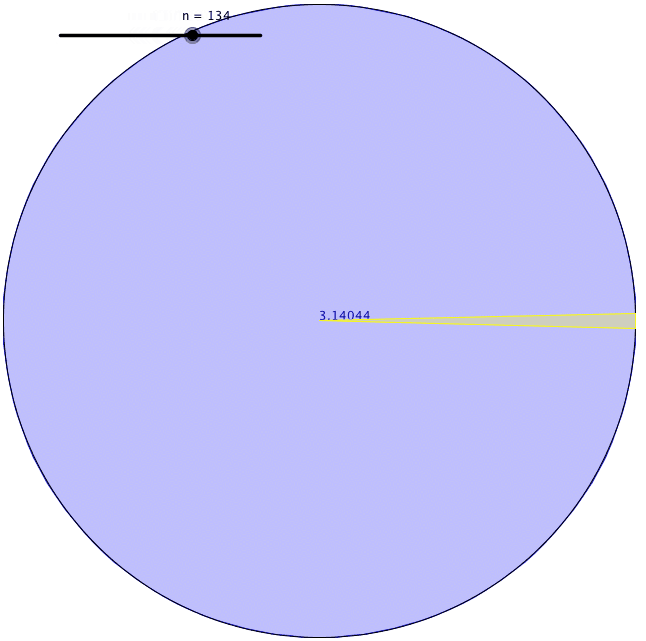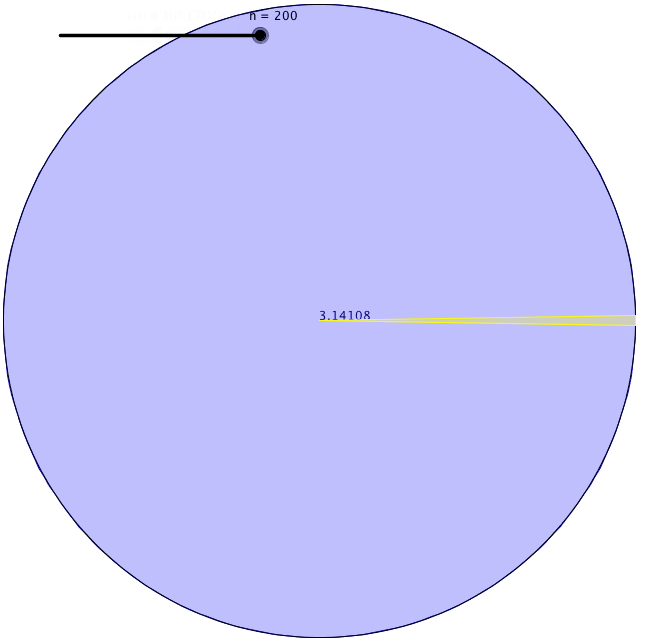
His definition is useful because measuring a curved surface was hard to do accurately. He found a way to find the circumference of a circle. First, he drew a square with its corners touching the perimeter of a circle and found the perimeter of the inscribed square. Secondly, he drew another square with its sides also touching the perimeter of the circle and found the perimeter of the circumscribed square. He came to the conclusion that the circumference of the circle had to lie somewhere between the value of those two perimeters of squares.
Using this method, however, the difference between those two values was pretty big. So, he drew pentagons to see the upper and lower bounds of the circumference of the circle. This gave him a smaller range of bounds. He kept increasing the number of faces of the polygon that he was drawing inside and outside the circle. Each time he did this, his estimation was getting more accurate. Archimedes got up to a 96 sided regular polygon [called an enneacontahexagon] until he grew exhausted. The lower and upper bound that he found were 3.1408 and 3.1429. Thus, he calculated π to two decimal places.
Archimedes’ method needed improvement because his life span was not going to be long enough to find the other digits of pi by hand. Mathematicians needed to discover more efficient formulas and new techniques.
Before they could do this, they needed to discover algebra. Its discovery by the great mathematicians inspired a whole new way of looking at the world.
The next great jump in calculating pi was the invention of calculus. After that, mathematicians started working on infinite series. An infinite series is an expression with numbers added together until infinity; sometimes these infinite series converge to a particular value.
There are many methods available now to calculate pi. Gottfried Leibniz found pi in infinity. James Gregory was working on one of the astonishing infinite series for the inverse tangent function below. He added infinitely many small numbers together and found pi.
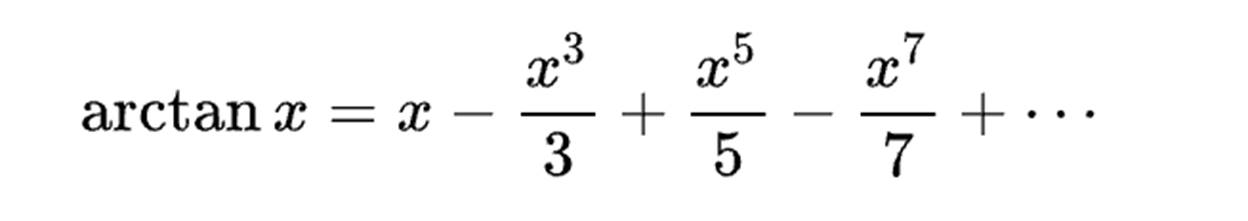
He put x = 1 into the inverse-tangent series. He showed us the further we go, the closer to the estimation of pi we get. However, in order to get 10 digits of pi, we need to write about 5 billion fractions.
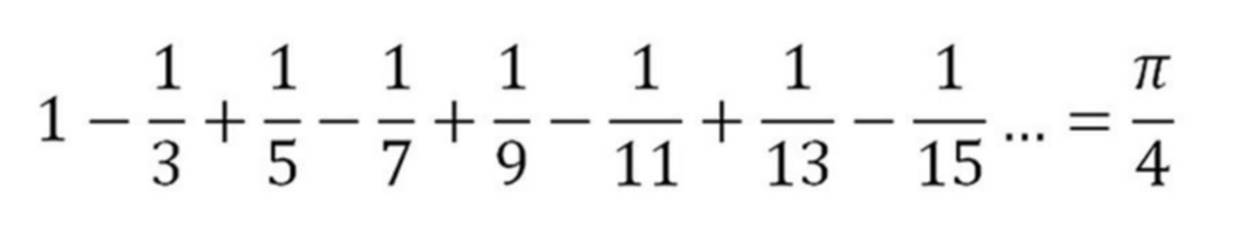
After that, another great mathematician, Leonhard Euler – who officially adopted the Greek letter “π” as a symbol to represent the value – found a more efficient equation for pi, when he was only 28. The symbol became iconic. Euler’s Pi equation calculates an infinite sum. The Basel Problem was named after him.
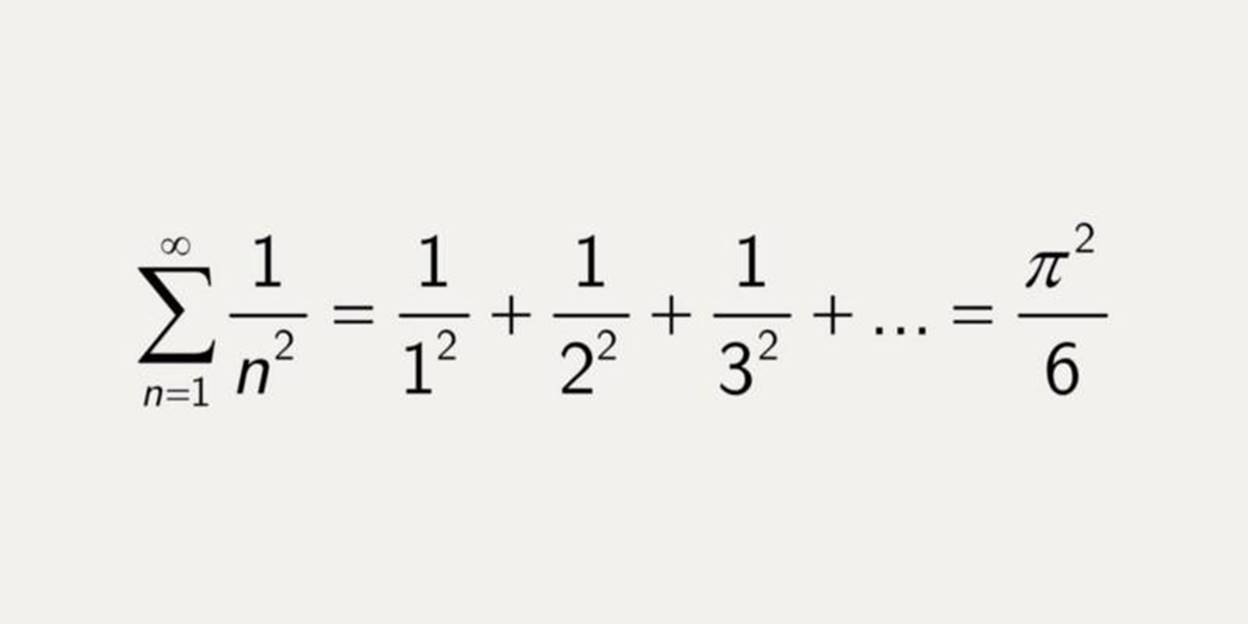
Euler also used pi to write another beautiful equation, Euler’s Identity.
![]()
Thanks to the Indian mathematician Ramanujan’s obsession with pi, we have many new formulas to find pi. When he arrived at Cambridge from India, he brought with him a notebook in which there were 400 pages of formulas to find pi.
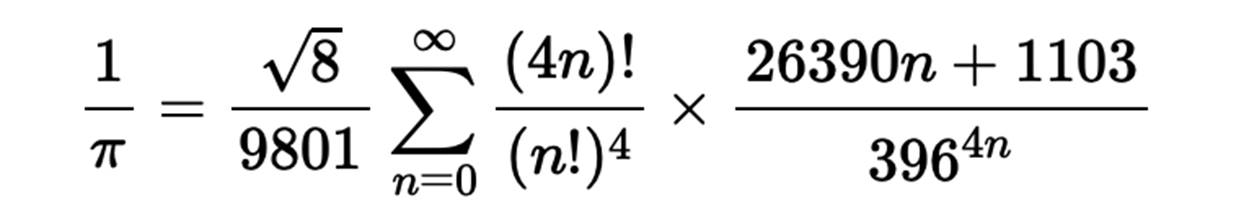
After the invention of mechanical computers, mathematicians used Leibniz’s, Euler’s, and Ramanujan’s infinite series to calculate a trillion decimal digits of pi (Stanford Cryptography Group). Without a supercomputer, finding this many digits of pi would be difficult. For example, the mathematician William Shanks managed to calculate the first 707 digits of pi by hand but unfortunately, he had made a mistake after the 527th place.
Pi is everywhere
Children start learning about pi when they are in 7th grade and use it until they graduate from college. Even after that, most people use pi again when their children go to school. Pi appears everywhere in the universe. It is literally woven into our universe: the orbits of planets, electromagnetic waves, rivers, the colors of auroras, the structure of DNA, the Great Pyramid of Giza... If a scientist wants to describe the structure of the universe or find the relationship between planets, he/she definitely needs to use pi: anything involving a circle or a sphere is about pi. Circles appear throughout the natural world, whether they’re a soap bubble or the moon in the night sky.

A Gif showing the clever play on the letters “pi”
Sinuosity of rivers
Pi has a direct relationship with rivers. But how? To figure this out, we need to measure the length of a river in two different ways. Assume that we know the starting and ending point of the river. First, we need the actual length to see how bendy the river is. In other words, the distance that you need to swim from the beginning point to the ending point. This whole length will be “L”. Second, we need to find a straight length. In other words, this time we need to fly from the beginning to the end. And this direct route will be a lowercase “l”. Now we can write the formula for the sinuosity by dividing L by l. The sinuosity is a ratio and measures how bendy the river is.
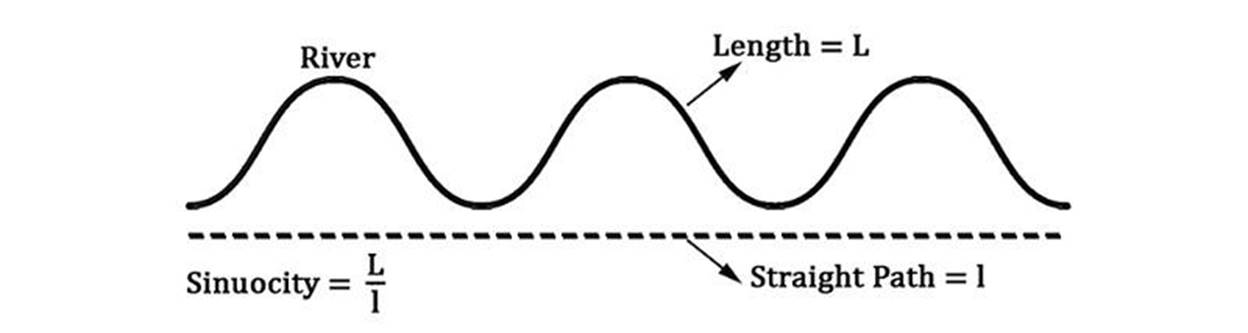
What is important here is there’s no limit to how high sinuosity can be. Rivers can be really bendy. However, Hans-Henrik Stølum proved that theaverage sinuosity of rivers around the world is pi. If you find the sinuosity of all the rivers and take the average sinuosity of them, you should get pi (Meandering River).
There is another interesting fact about sinuosity. Rivers can be very bendy at some points. But suddenly, those rivers become straight and make the sinuosity around pi. So, it is hard to find the sinuosity of a river equal to 7 because of fluid dynamics. Mathematicians found the highest sinuosity to be around 3.5 and the lowest sinuosity around 2.7.
At the extremely bendy point, rivers cut off after the bend point and make a shortcut to become straight again. This phenomenon is known as an oxbow lake, which controls the sinuosity of rivers. This keeps the sinuosity of a river around Pi.


Pi in Space
There is a mathematical order inherent in our universe. For instance, to understand our solar system, we need pi. We know that our planet moves in front of its host star. And the light comes from host stars. To talk about that light, we need to know how big the host star is. In other words, we need the surface area of the host star. The formula for the surface area of a sphere is 4πr², with r being the star’s radius. The size of a planet also helps scientists to guess whether it is habitable or not.
Another good example to show the relationship between pi and the universe is electrostatic force, which is the force between two electric charges. An electron exerts a force in all directions and forms a sphere field. Electrons also interact with each other on an electric field. To figure out that interaction, we need to find the surface area of spheres, where again pi comes up.
There is also a connection between pi and gravity. If you have had a chance to see Einstein’s field equations, you might notice that pi is there also:
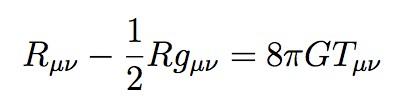
The formula above calculates how objects with a large mass, such as stars and galaxies, can curve space and time with their gravity. Einstein said that, just like a ball sitting on a bedsheet, any form of momentum and energy can also curve space-time around it. In words, the formula is saying:
Gravity = 8 x π x Energy & Momentum
Lastly, if you take the square root of Earth’s gravity, you almost get pi.
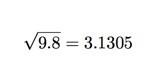
Pi Day
After so many years studying pi, people decided to organize an official celebration of pi on March 14th. Since 1988, people have celebrated this magical constant. Coincidentally, Albert Einstein was born on pi day – March 14, 1879. Einstein also published his theory of general relativity on pi day.

 The Google logos for Pi Day.
The Google logos for Pi Day.